
Physics 포스팅
Doyeon0430 | 2023년 09월 14일
이번시간에는 통계학 단원 중 자료의 종류를 소개하겠습니다.
자료는 크게 질적 자료와 양적 자료 두 가지로 나눌 수 있습니다.
두 개념에 의미를 해석해보고 각각의 차이점을 알아보겠습니다.
그럼 지금부터 포스팅을 시작합니다.
질적 자료와 양적 자료에 차이점을 알아보겠습니다.
범주형 자료로 분류되며 순위형 자료와 명목형 자료가 있습니다.
순위형 자료 : 학년, 평점처럼 카테고리 간 순서가 있는 자료입니다.
명목형 자료 : 혈액형, 성별처럼 카테고리 간 순서가 없는 자료입니다.
수치형 자료로 분류되며 연속형 자료와 이산형 자료가 있습니다.
연속형 자료 : 비율척도랑 구간척도가 있고 대부분 사칙연산이 가능한 비율척도를 사용합니다.
이산형 자료 : 주사위 결과처럼 특정 범위 내에서 값이 제한된 자료를 나타냅니다.
질적 자료는 그래프나 도표를 통해 정리하며 내포된 정보를 쉽고 빠르게 전달할 수 있습니다.
도수란 각 자료값이 나타나는 빈도수를 나타냅니다.
상대도수는 이 도수를 전체 자료의 숫자로 나눈 것입니다.
그래서 도수나 상대도수를 나열해 놓은 도표를 도수분포표라고 합니다.
상대도수 = 도수 / 데이터 수
각 자료값의 상대도수를 같은 폭의 막대로 나타냅니다.
그래서 막대의 높이는 상대도수 크기에 비례합니다.
도수분포표를 시각화하기 위해 사용되는 그래프입니다.
각 조각의 크기는 해당하는 자료값의 상대도수에 비례합니다.
양적 자료도 질적 자료처럼 도표나 그림을 통해 자료의 분포상태를 나타냅니다.
제일 먼저 자료의 줄기부분을 선택해야 합니다.
줄기부분을 제외한 나머지 부분을 잎이라고 합니다.
86 65 74 63 71
61 59 85 77 84
87 75 53 81 68
75 98 62 89 74
91 57 66 94 70
87 73 78 93 67위와 같은 경우 십 자릿수는 줄기가 되며 일 자릿수는 잎이 됩니다.
이 다음으로 크기를 나열해 줍니다.
5 | 3 7 9
6 | 1 2 3 5 6 7 8
7 | 0 1 3 4 4 5 5 7 8
8 | 1 4 5 6 7 7 9
9 | 1 3 4 8적정 줄기 개수는 자료의 크기에 따라 다르며 5~20개 사이를 선택합니다.
첫 번째 장점은 언제든지 원래 자료값을 줄기-잎-그림으로부터 얻을 수 있습니다.
두 번째 장점은 크기순으로 나열하는 것이 용이해서 특정 위치 자료값을 쉽게 구할 수 있습니다.
첫 번째 단점은 적절한 줄기의 개수를 정하기 어렵습니다.
두 번째 단점은 자료집합의 크기가 클 때는 적절하지 않습니다.
양적 자료에서 도수분포표는 서로 인접한 자료값들을 집단화하여 전체 자료집합을 몇 개의 그룹으로 나누면 됩니다.
그럼 지금부터 도수분포표 작성 방법에 대해 알아보겠습니다.
계급번호(k) 계급구간(h) 도수 상대도수
1 52.5~60.5 3 0.10
2 60.5~68.5 7 0.23
3 68.5~76.5 7 0.23
4 76.5~84.5 4 0.13
5 84.5~92.5 6 0.20
6 92.5~100.5 3 0.10[1번째]
데이터를 수집하는데 개수는 50~100개가 적당합니다.
[2번째]
데이터 개수에 따라 적당한 계급의 수(k)를 정해줍니다.
계급의 수(k) = 경험치를 토대로 구해주는게 좋습니다.
[3번째]
수집한 데이터에서 최대치와 최소치를 구해줍니다.
[4번째]
최대치와 최소치를 이용해 범위(R)를 구해줍니다.
범위(R) = 최대치 - 최소치
[5번째]
계급구간에 폭(h)을 구해줍니다.
계급의 폭(h) = (최대치 - 최소치) / 계급의 수(k)
여기서 소수가 나온다면 최소단위의 정배수를 배정합니다.
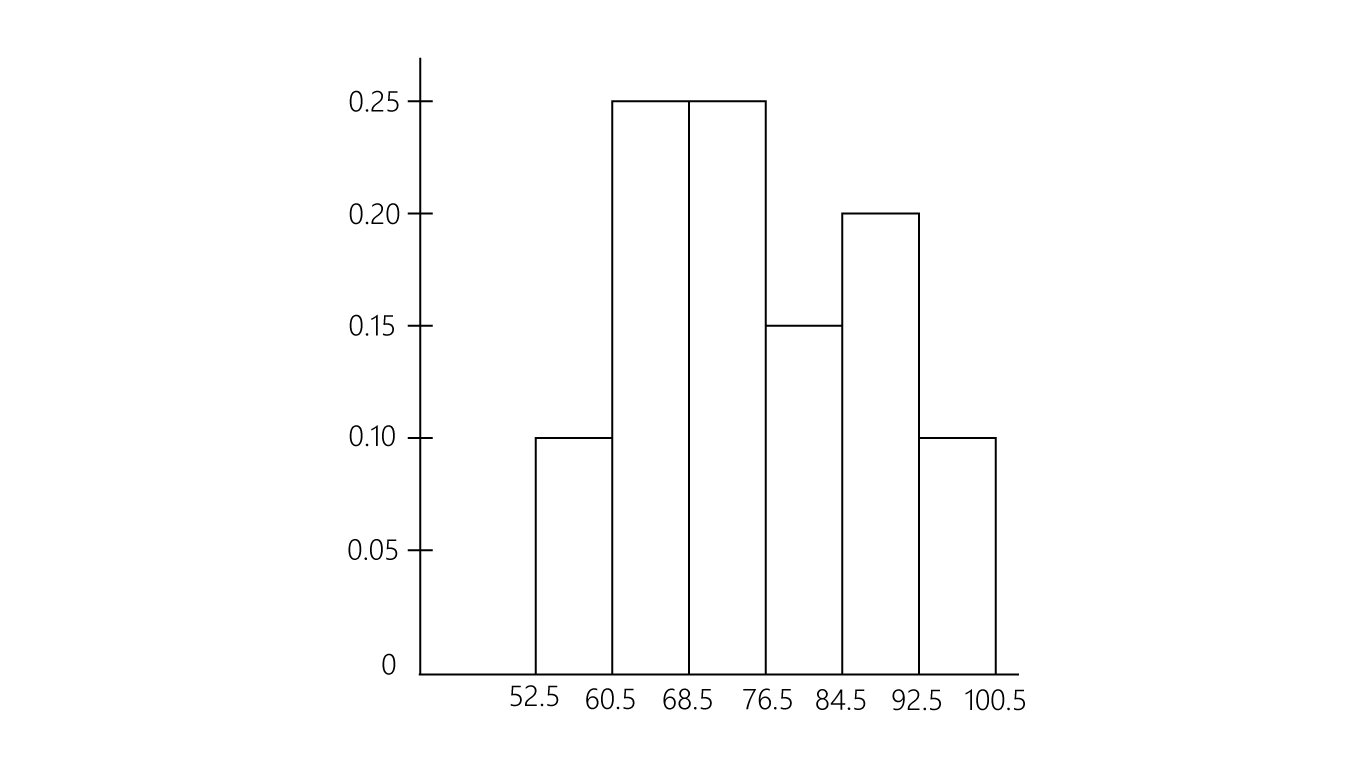
위에서 구한 도수분포표를 그림으로 표현하는 방법이 히스토그램입니다.
히스토그램은 줄기-잎-그림을 시계반대방향으로 90도 회전시킨 것과 비슷합니다.
각 계급의 도수 또는 상대도수를 그 크기에 따라 막대로 표현한 그래프입니다.
산포는 왜도와 첨도 시 사용하는 척도로 작은 쪽이 정밀도가 좋습니다.
만약 규격상한이나 규격하한에 근접한다면 산포를 줄여야 하고 초과하면 정확도를 높여야 합니다.
또한 상대도수를 나누어줬을 때 상대도수밀도로 이용해야합니다.
상대도수밀도 = 계급의 상대도수 / 계급의 간격
히스토그램에 각 막대의 윗 부분 중간점에서 직선으로 연결한 그래프입니다.
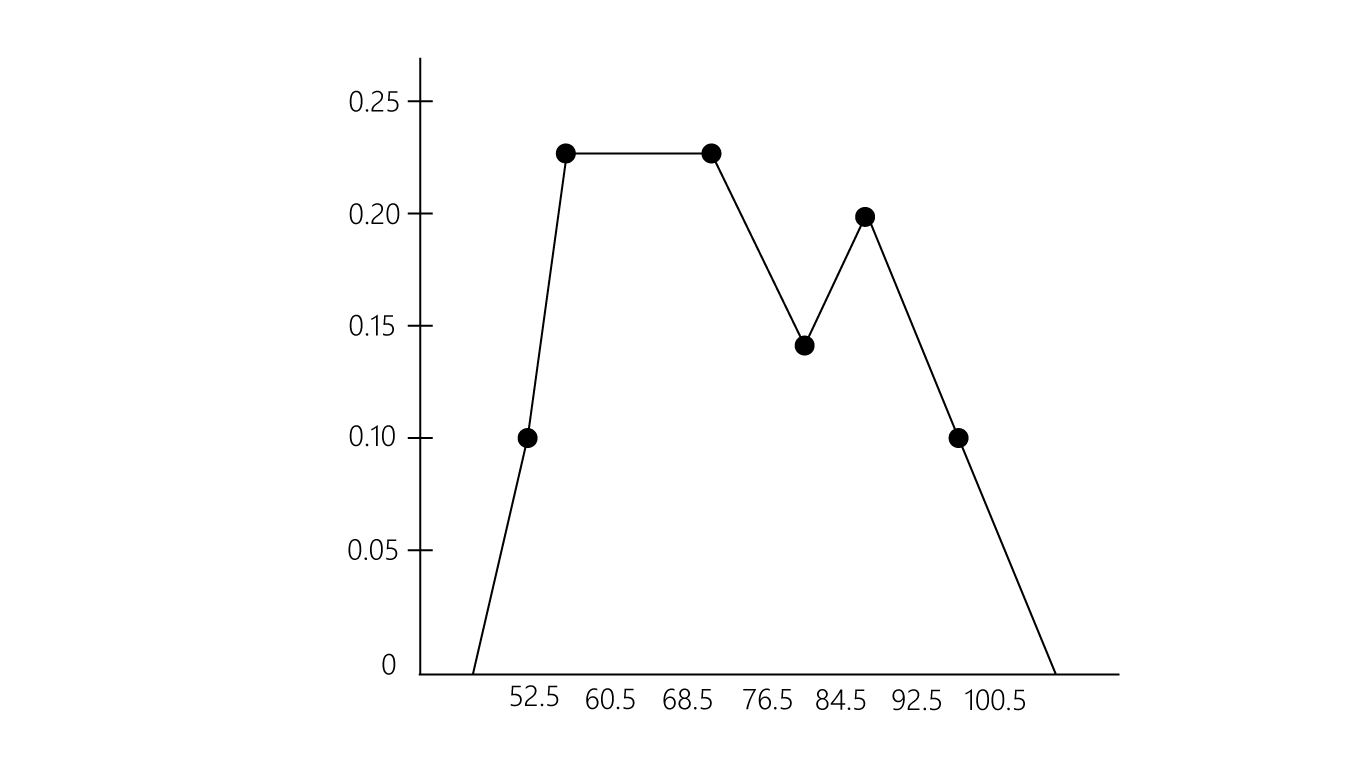
두 개 이상의 자료집합의 분포를 같은 그림 위에 놓고 비교할 수 있어 편리합니다.
댓글 (0)
간편 댓글 작성





