
Physics 포스팅
Doyeon0430 | 2023년 09월 17일

이번시간에는 선형대수학에 기본적인 개념인 행렬에 대해 소개하겠습니다.
행렬은 숫자를 직사각형 모양의 배열로 나타낸 것을 의미합니다.
수학뿐만 아니라 공학이나 과학적으로 다양한 분야에서 쓰이고 있습니다.
그럼 지금부터 행렬의 개념과 연산 그리고 가우스 소거법을 알아보겠습니다.
행렬은 연립일차방정식을 표현하면서 행렬을 사용할 때 쉽게 풀 수 있습니다.
대표적으로 나와있는 기본 행 연산에 3가지 공식이 있습니다.
1. 두 행을 서로 교환할 수 있습니다.
2. 0이 아닌 상수를 한 행에 곱할 수 있습니다.
3. 한 행에 상수를 곱한 것을 다른 행에 더할 수 있습니다.
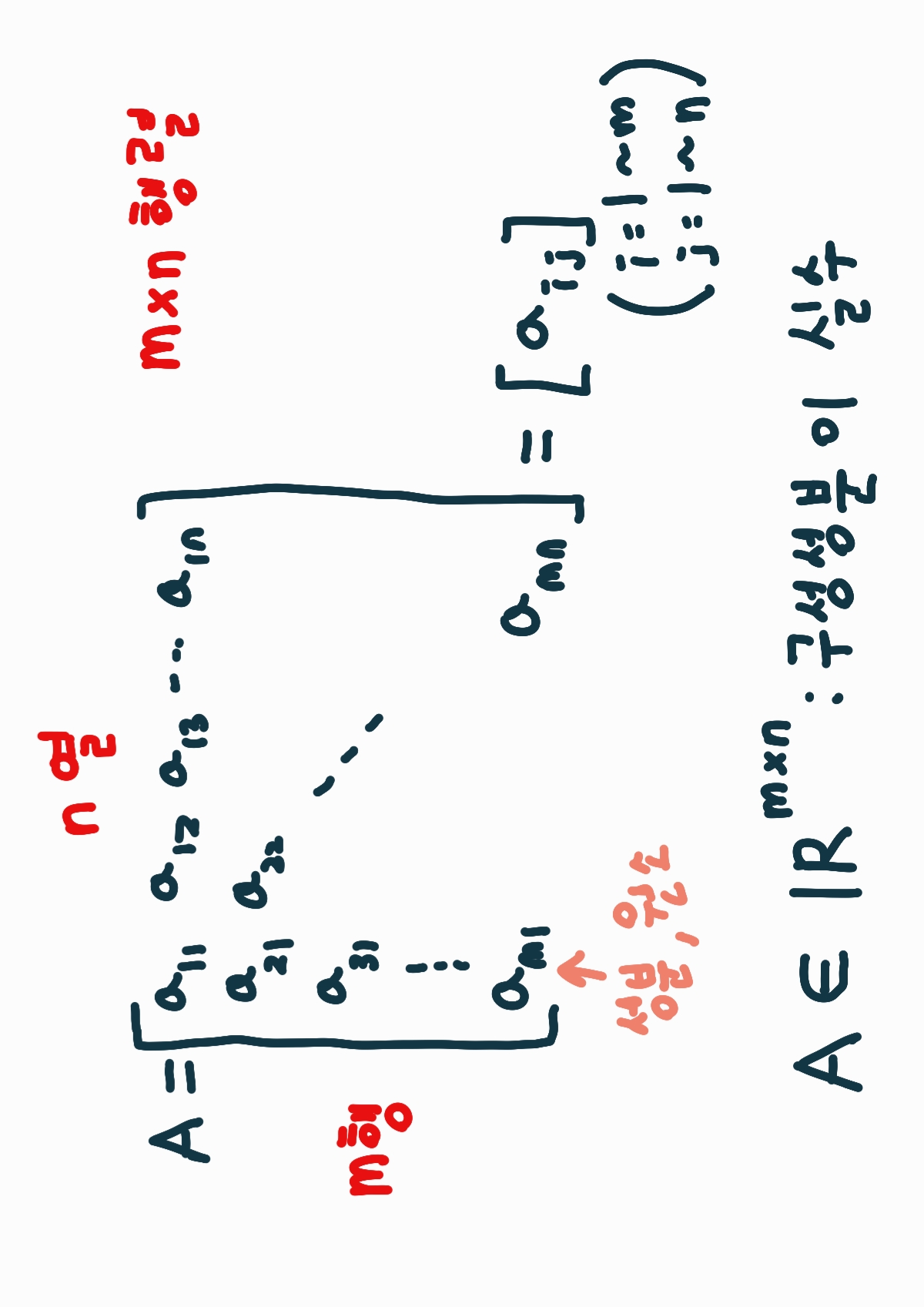
행렬은 대괄호로 묶인 숫자의 배열로 가로줄은 행이며 세로줄은 열이라고 부릅니다.
위의 사진은 m행과 n열로 구성된 행렬의 기본 구조입니다.
그리고 배열한 숫자를 행렬의 성분이나 원소라고 합니다.
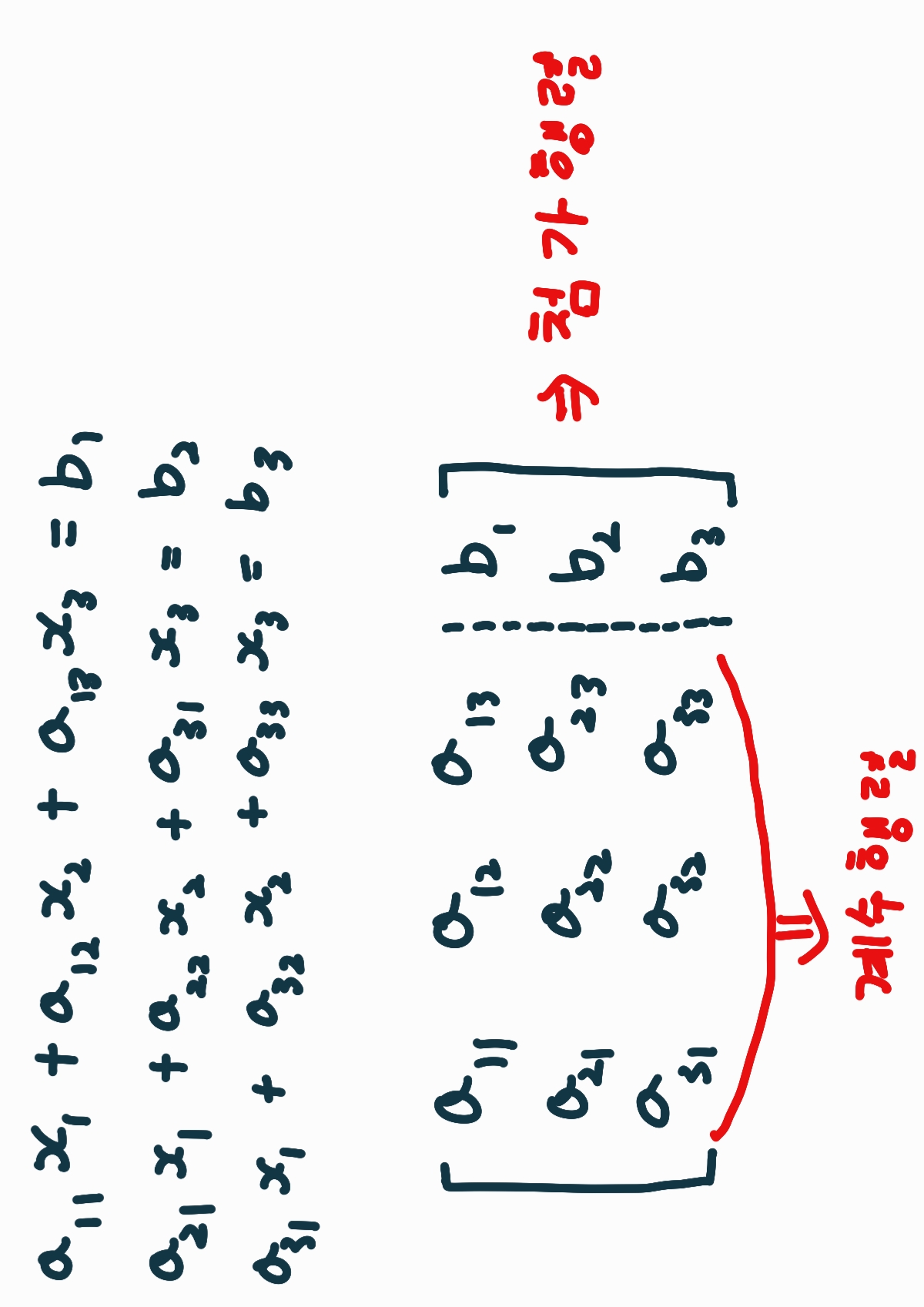
계수행렬은 연립일차방정식에 x와 y 계수의 값들을 행렬로 나타낸 표현식입니다.
여기서 우변의 상수를 포함한 행렬을 첨가행렬이라고 합니다.
두 개의 값은 수직선으로 구분하여 나타냅니다.
위에서 말한 기본 행 연산을 통해 가우스 소거법을 사용할 수 있습니다.
가우스 소거법은 첨가행렬을 이용해 미지수를 구하는 방법입니다.

위의 식은 가우스 소거법을 사용하여 값을 구한 풀이과정입니다.
1번 풀이는 1행에서 2, 3행에 곱셈을 넣어줍니다.
2번 풀이는 2행에서 3행에 곱셈을 넣어줍니다.
3번 풀이에서 3행 3열 값에 1을 만들어 줍니다.
4번 풀이는 3행에서 2행에 곱셈을 넣어줍니다.
5번 풀이에서 2행 2열 값에 1을 만들어 줍니다.
6번 풀이는 2, 3행에서 1행에 곱셈을 넣어줍니다.
이렇게 풀이가 끝났으며 기약행사다리꼴 형식으로 만들어졌습니다.
기약행사다리꼴을 만족하기 위해서는 4가지 조건이 필요합니다.
1. 각 행의 0이 아닌 첫 성분은 1이며 선행 1이라고 부릅니다.
2. 모든 성분이 0인 행은 행렬의 마지막 행으로 둡니다.
3. 선행 1이 있는 열의 나머지 성분은 0입니다.
4. 모든 성분이 0이 아닌 인접한 두 행의 선행 1은 왼쪽 상단에서 오른쪽 하단으로 구성됩니다.
마지막으로 행렬의 기본 연산들을 알아보겠습니다.
행렬의 크기는 행의 개수와 열의 개수로 결정됩니다.
여기서 행과 열의 개수가 같으면 정사각행렬이라고 부릅니다.
그리고 성분 a12은 1행 2열이라고 나타냅니다.
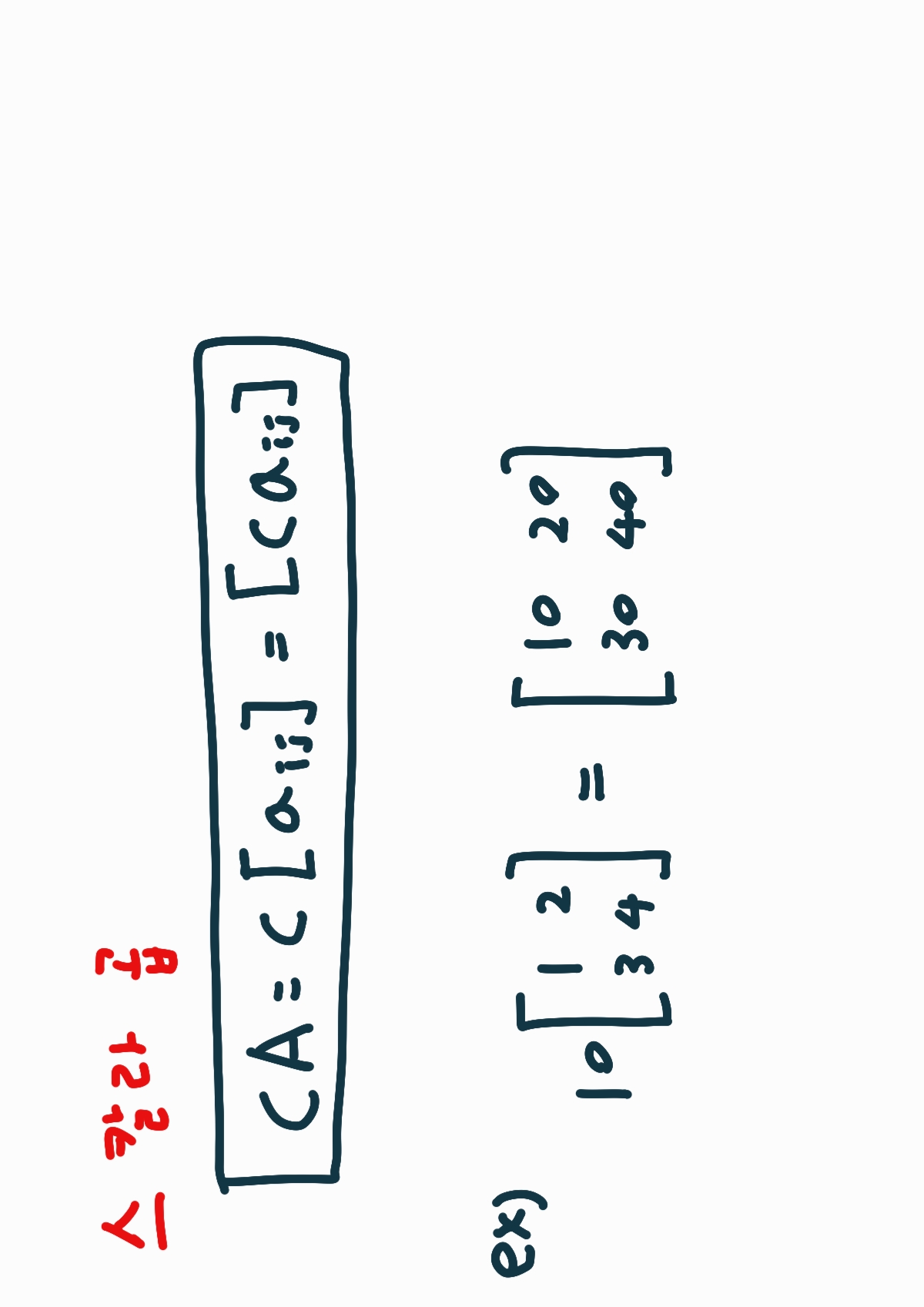
행렬의 모든 원소에 스칼라를 곱하는 연산입니다.
여기서 aij는 행렬 A의 원소이며 c는 스칼라입니다.
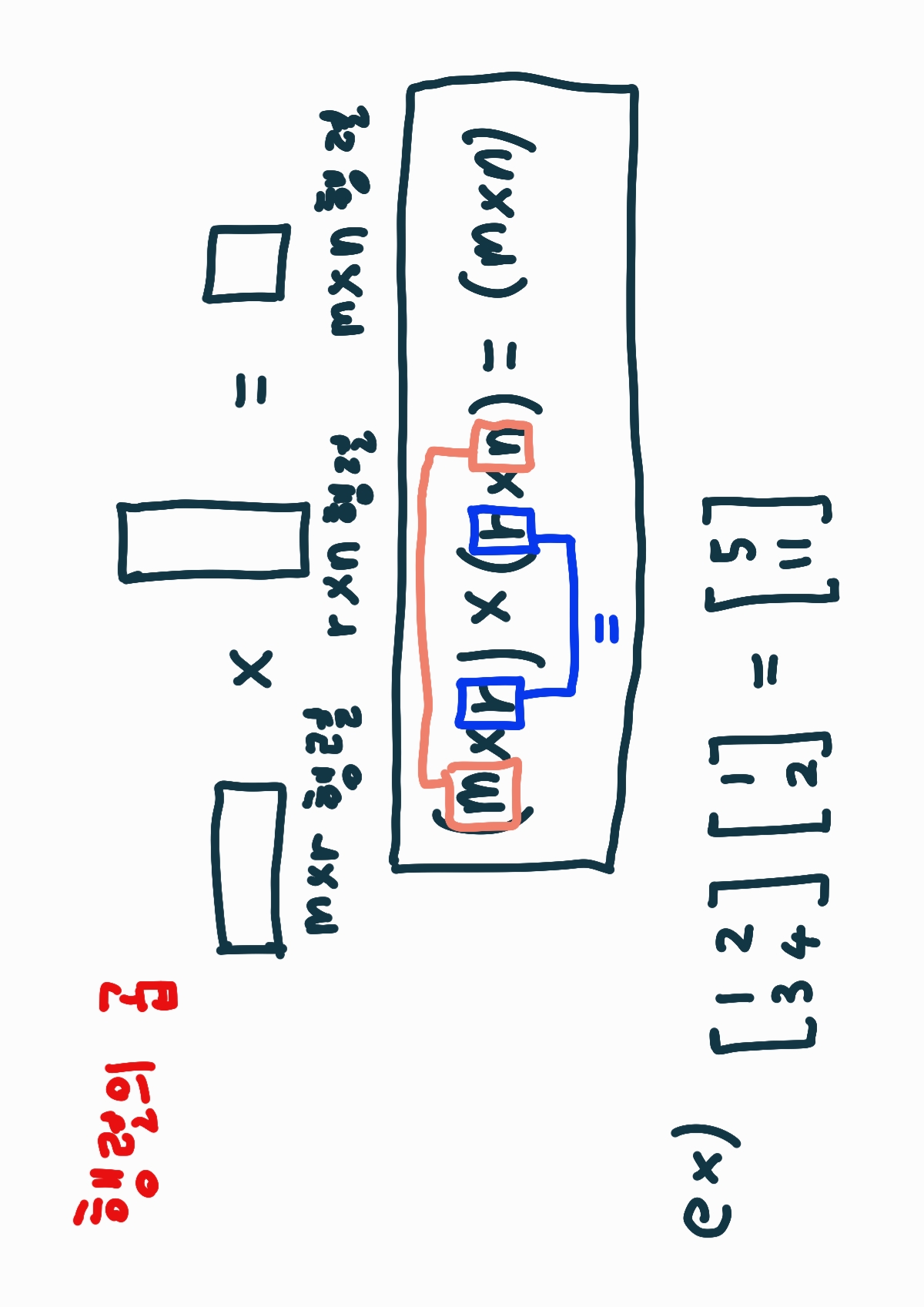
두 개의 행렬을 곱하는 연산입니다.
첫 번째 행렬의 열과 두 번째 행렬의 행을 조합하여 새로운 행렬을 만듭니다.
그래서 행렬의 곱셈은 교환법칙이 성립되지 않습니다.

두 개의 행렬을 더하거나 빼는 연산입니다.
두 행렬의 크기와 구조가 동일해야 합니다.

행렬과 벡터를 곱하는 연산입니다.
행렬 A와 열 벡터 x를 곱하면 새로운 열 벡터 Ax가 생성됩니다.
댓글 (0)
간편 댓글 작성





