
Physics 포스팅
Doyeon0430 | 2023년 11월 01일

이번시간에는 동역학에 직각좌표계와 운동방정식을 알아보겠습니다.
동역학은 물체의 움직임을 이해하고 예측하는 데 중요한 도구 중 하나입니다.
이러한 이해를 통해 일상에서 경험하는 운동 현상을 더 깊게 파헤칠 수 있습니다.
그럼 지금부터 포스팅을 시작하겠습니다.
직각좌표계 또는 데카르트좌표계라 불리며 현재 가장 널리 사용하는 좌표계입니다.
x축과 y축이 수직으로 교차하며 점이나 벡터를 나타날 수 있습니다.
직선운동 또는 직선운동의 중첩으로 묘사될 수 있는 운동에 적합하며 투사체운동이 이에 속합니다.
운동방정식은 뉴턴의 제2법칙을 기반으로 하는 방정식입니다.
이 방정식으로 질점의 힘과 가속도의 관계를 알아보며 힘-질량-가속도로 정의합니다.
힘-질량-가속도를 사용할 때는 자유물체 선도(FBD)와 질량-가속도 선도(MAD)를 표시합니다.
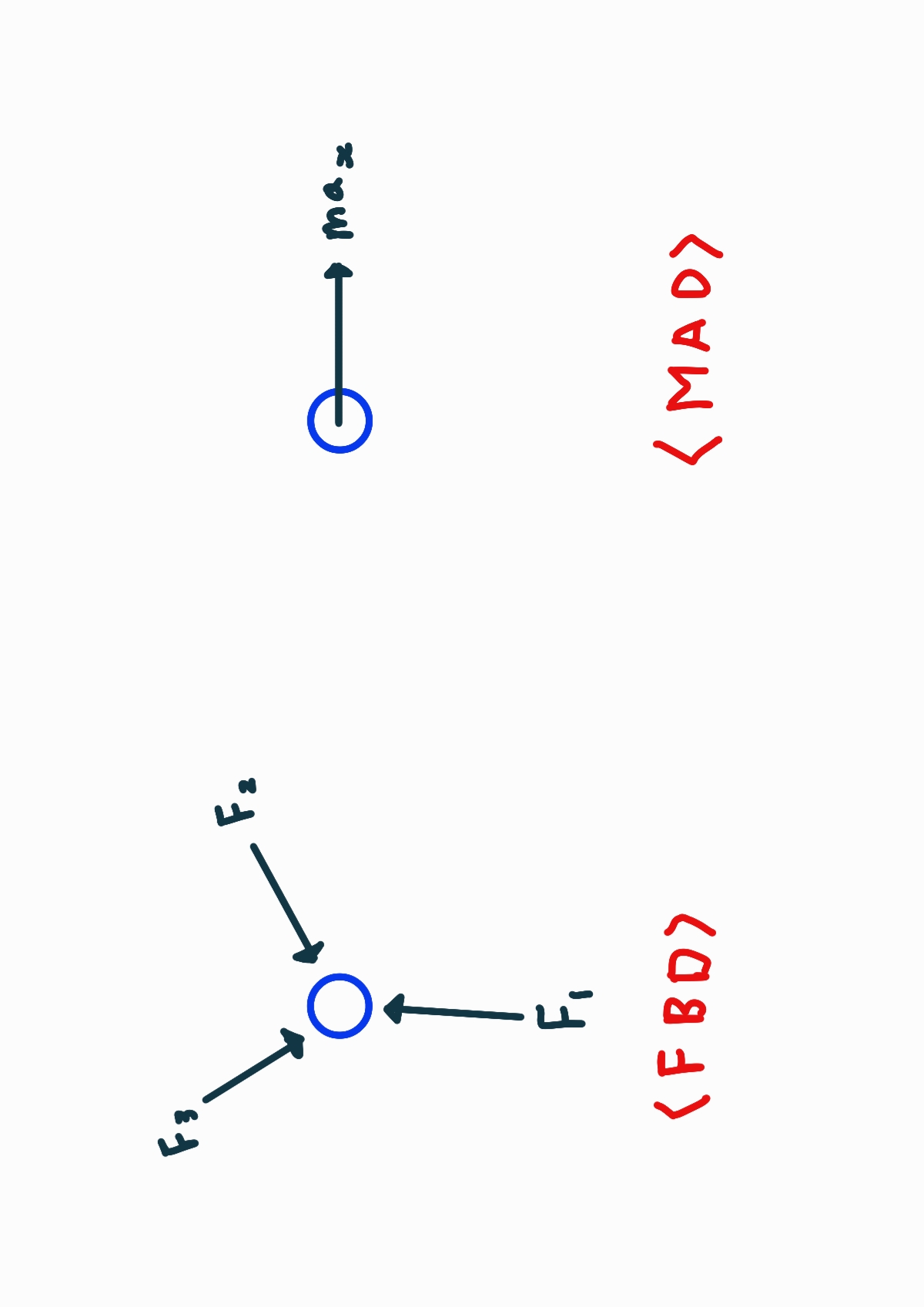
선도를 통해서 모든 힘들에 관계를 분명하고 정확하게 나타낼 수 있습니다.
다음으로 운동방정식에 위치, 속도, 가속도 관계를 알아보겠습니다.

가속도가 주어진 상황에서 위치와 속도를 구할 수 있습니다.
여기서 나오는 적분상수는 초기 시간이나 초기 위치를 통해 구하면 됩니다.
문제에서 가속도가 일정할 때는 적분을 이용하고 그 외에는 연쇄법칙을 사용해 속도를 유도합니다.
자유물체 선도와 질량-가속도 선도를 통해 동역학 예시문제를 풀어보겠습니다.
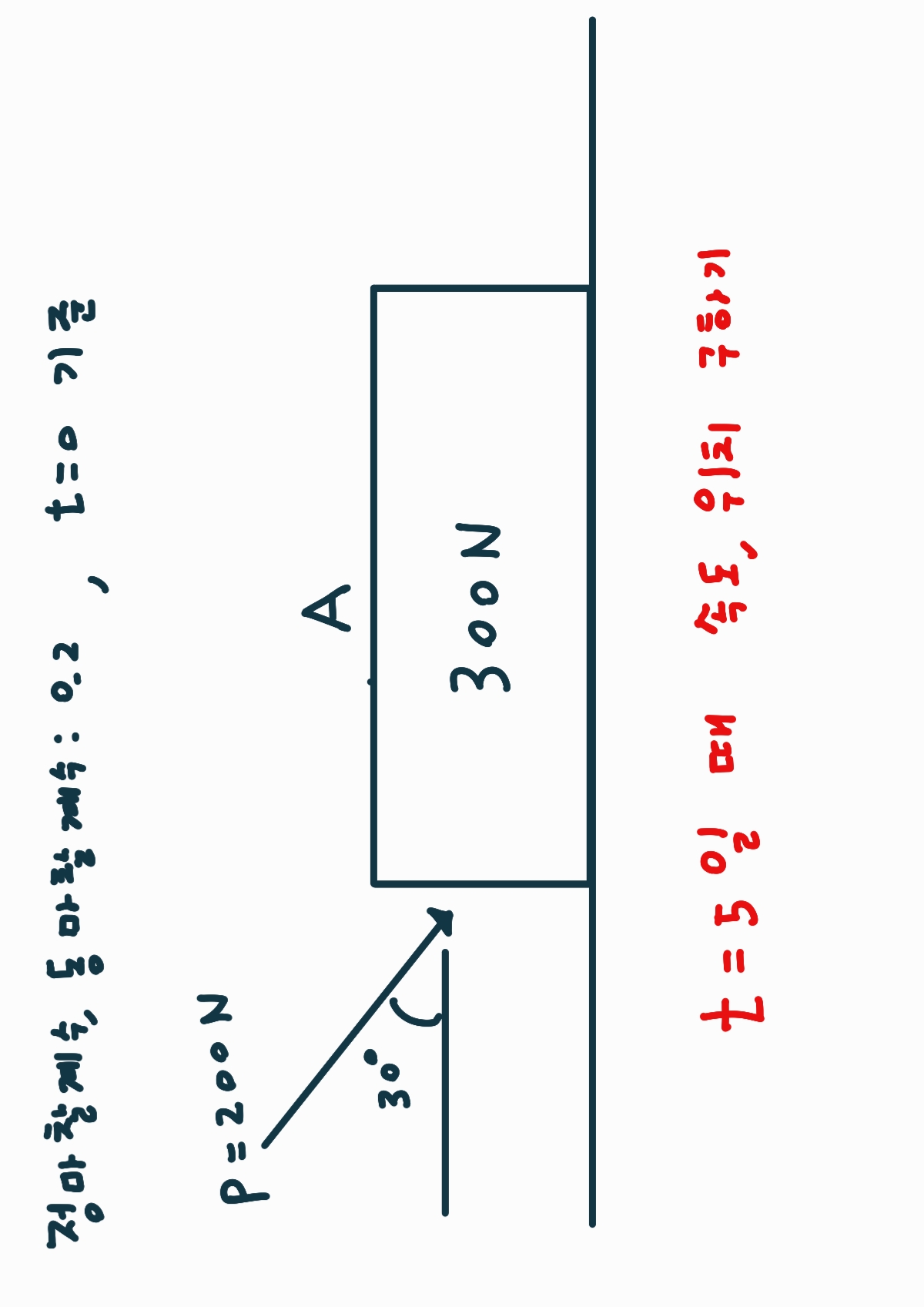
정마찰계수는 정지해 있을 때 마찰계수이며 동마찰계수는 움직일 때 발생하는 마찰계수입니다.
또한 마찰계수는 항상 힘에 반대방향으로 향합니다.
t=0에서 P에 방향으로 200N을 준다는 가정이며 t=5일 때 위치와 속도를 구하겠습니다.
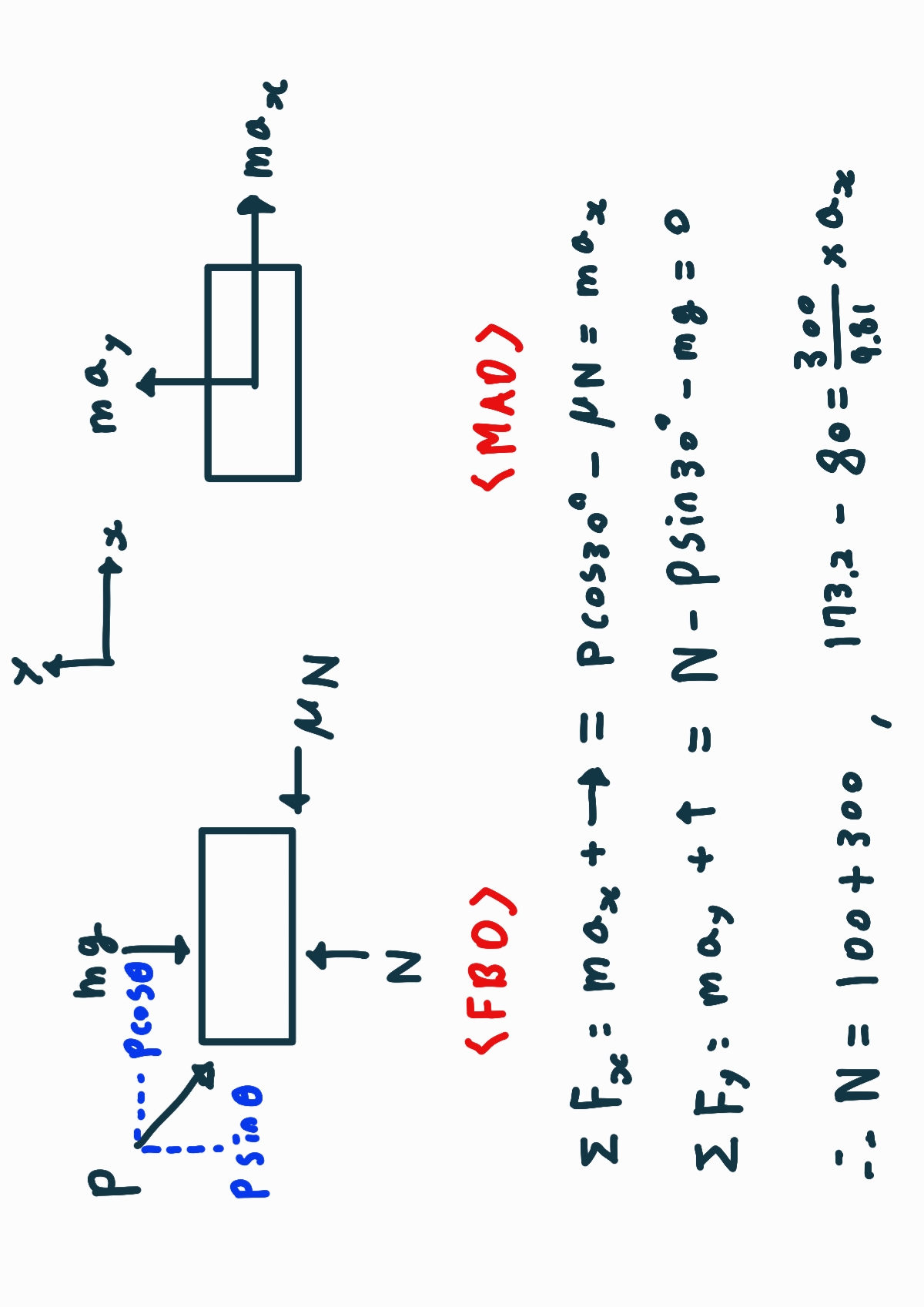
FBD와 MAD에 그림을 나타내며 힘의 방향을 표시합니다.
그리고 x축과 y축으로 나누고 아래 식을 작성합니다.
그럼 N(수직항력)과 a(가속도)에 값을 구할 수 있습니다.
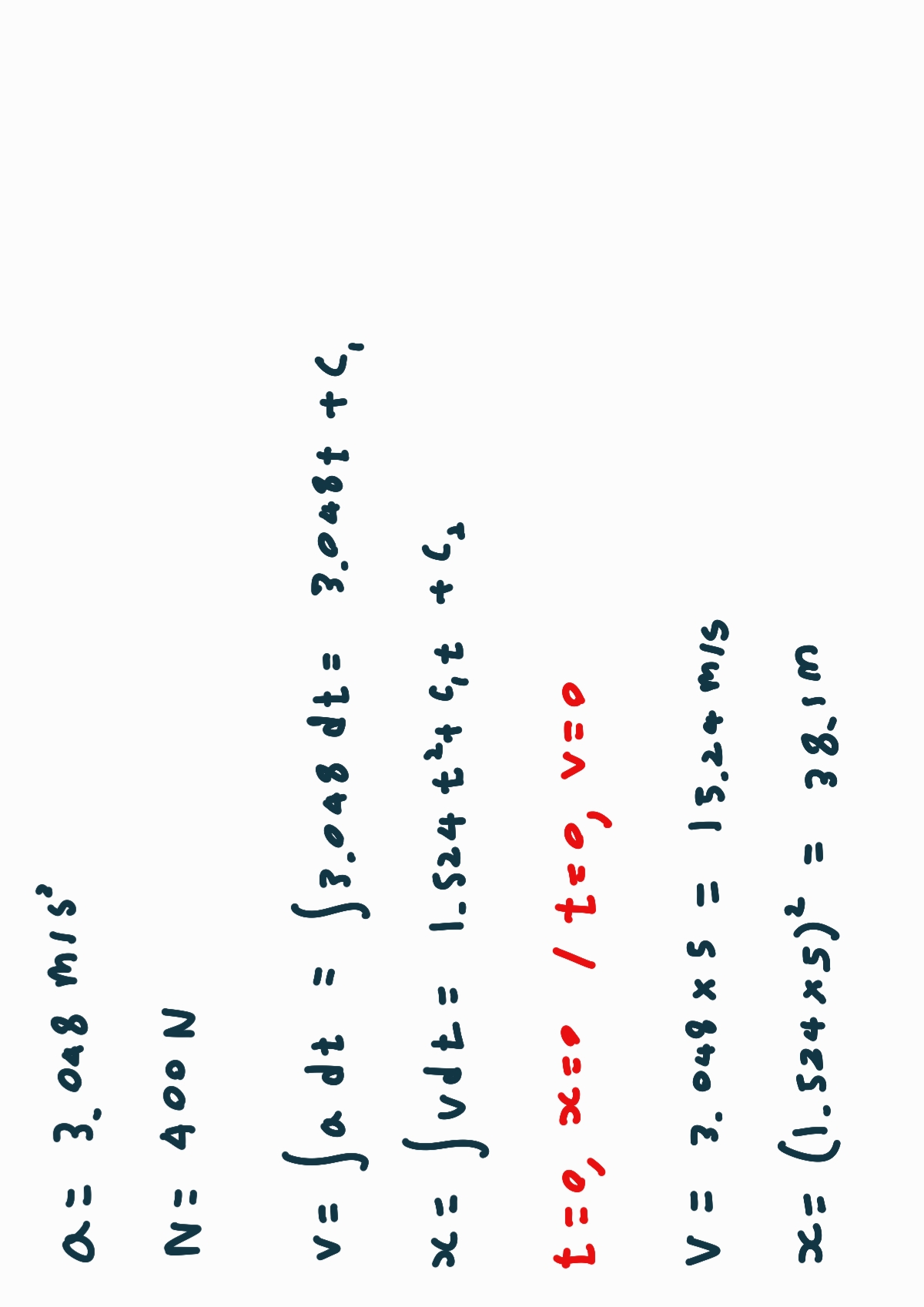
가속도는 방해없이 일정하므로 적분을 사용합니다.
시간이 0초일 때 위치와 속도가 원점에서 정지이므로 적분상수는 사라집니다.
이를 통해 시간이 5초에서 속도와 위치를 구할 수 있습니다.
댓글 (0)
간편 댓글 작성





