
Physics 포스팅
Doyeon0430 | 2023년 09월 16일

이번시간에는 직각좌표계에 기본적인 개념인 벡터를 정리하겠습니다.
벡터란 크기와 방향을 가지고 양을 나타낸 수학적인 개념입니다.
일반적으로 물리학 및 수학적인 공식 등 다양한 분야에서 자주 활용됩니다.
그럼 지금부터 벡터의 개념과 벡터의 내적과 외적을 소개하겠습니다.
벡터는 크기와 방향을 동시에 가지고 있으며 화살표를 사용해서 나타냅니다.
아래는 속력과 속도의 차이입니다.
속력 : 크기만 가진 스칼라
속도 : 크기와 방향을 가진 벡터
이외에도 벡터는 교환법칙과 결합법칙 등이 가능합니다.
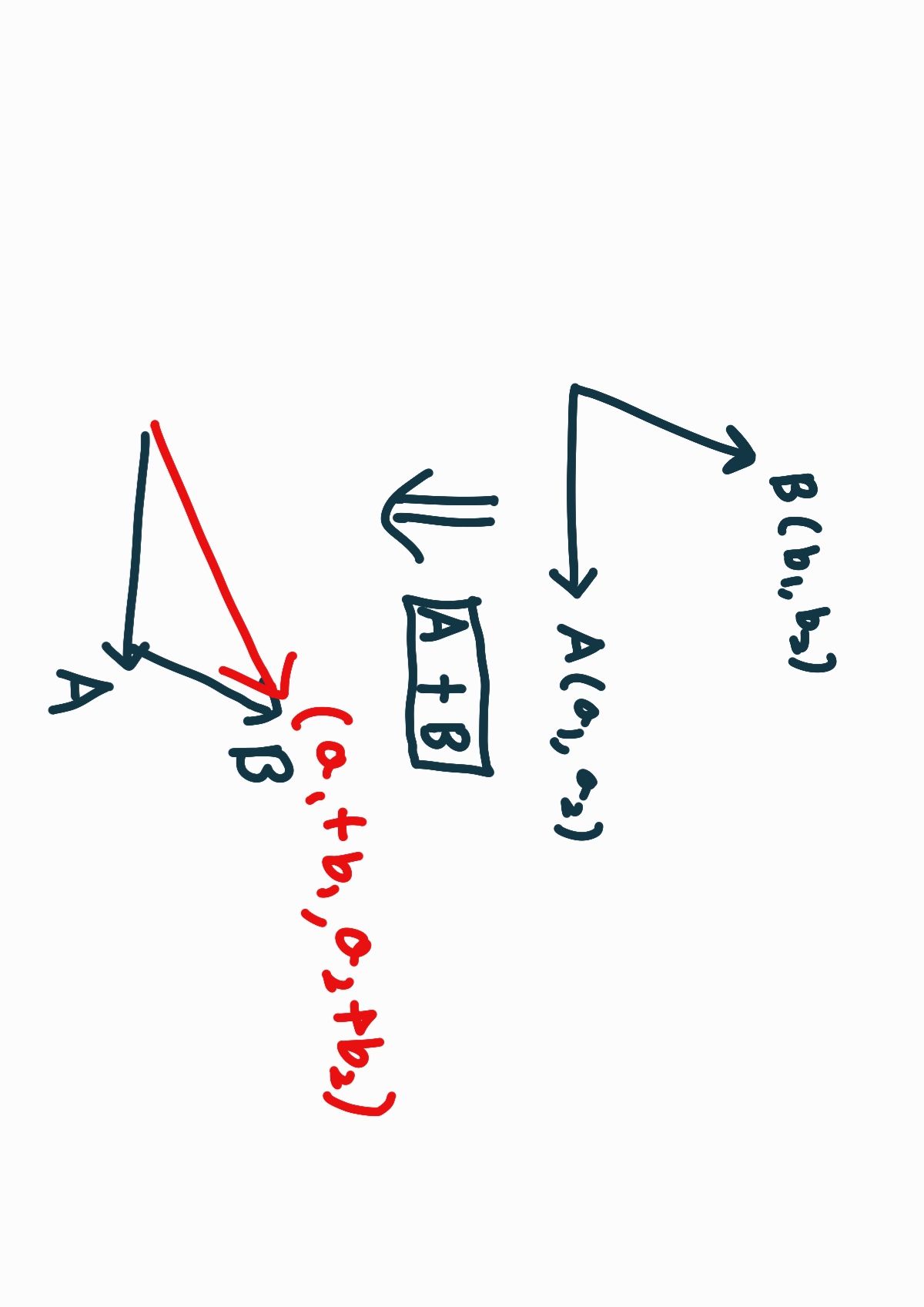
벡터의 덧셈은 두 개 이상의 벡터를 결합하여 새로운 벡터를 만듭니다.
기본적으로 머리끝에서 꼬리끝으로 연산을 수행합니다.
벡터의 머리를 시작으로 다른 벡터의 꼬리에 연결하여 새로운 벡터를 생성할 수 있습니다.
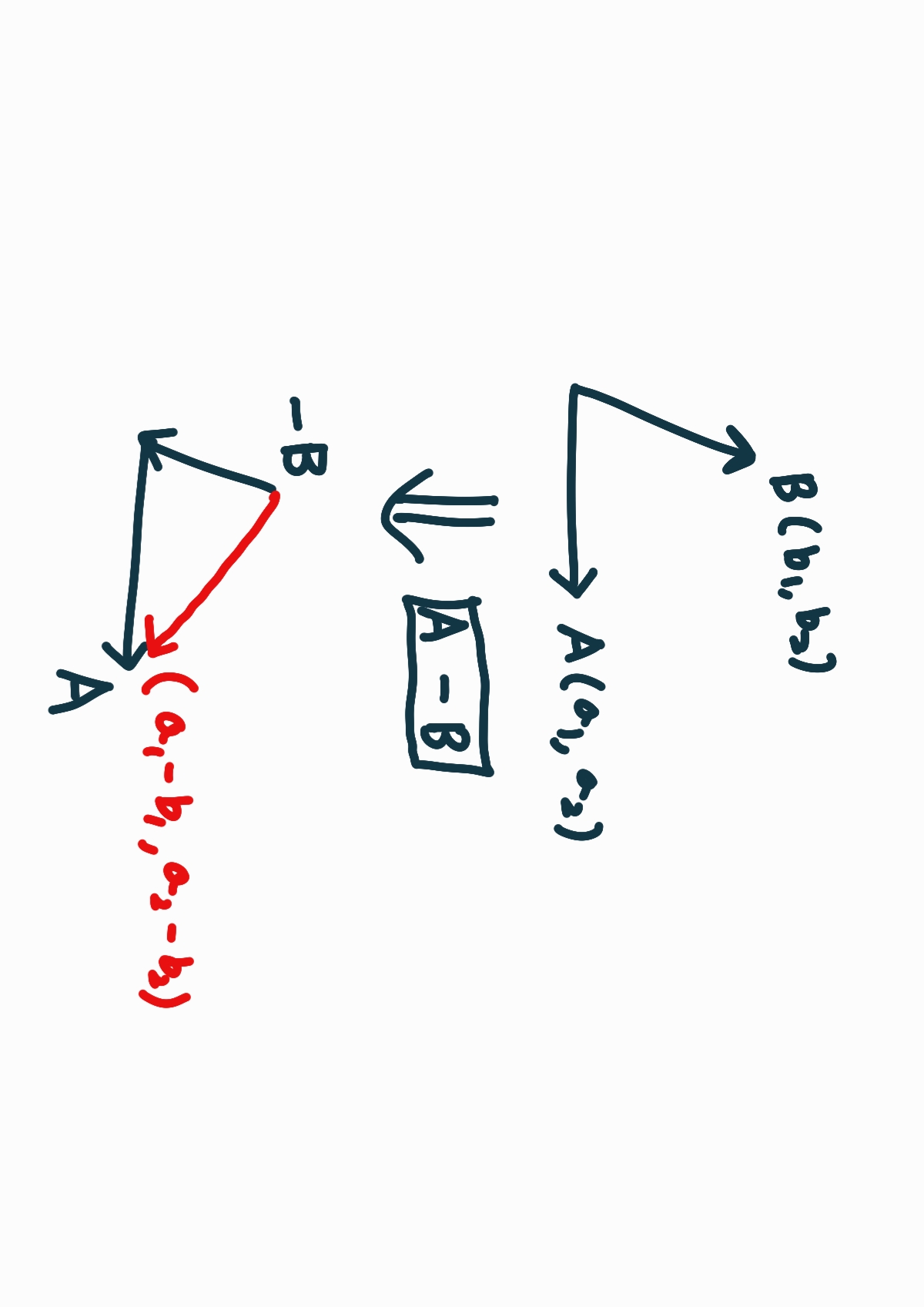
벡터의 뺄셈은 두 벡터 간의 차이를 구하는 연산입니다.
벡터 b를 벡터 a에서 뺄 때 b를 반대 방향으로 설정합니다.
그리고 벡터 a와 -b를 덧셈으로 계산하면 됩니다.
벡터 b의 반대 방향은 -b로 표시할 수 있습니다.
벡터의 내적은 두 벡터 간의 내적 연산을 한 것으로 스칼라곱이 나옵니다.
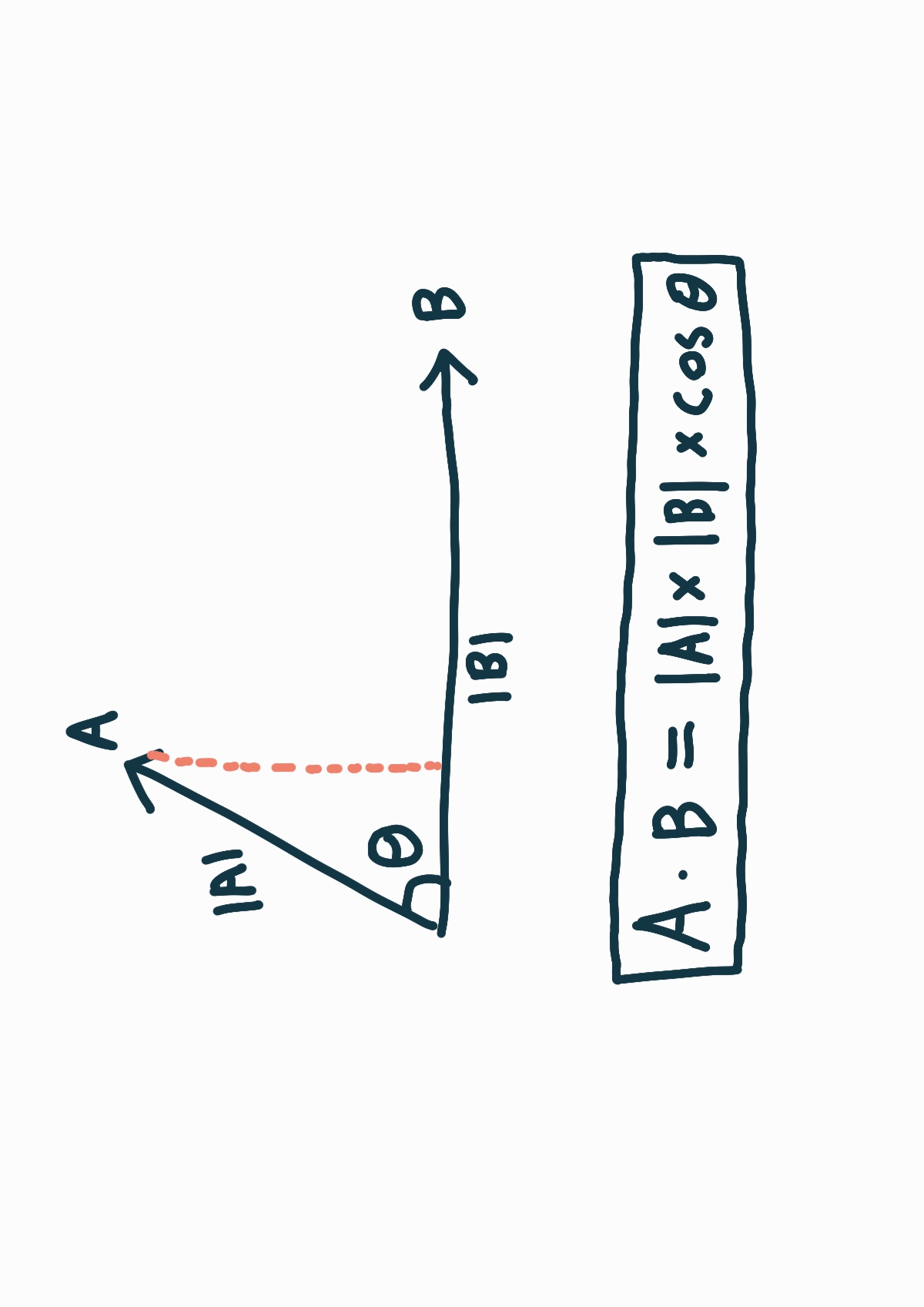
벡터 a와 b 사이의 각도가 θ이 주어지면 벡터의 내적을 구할 수 있습니다.
여기서 벡터의 내적은 크기만 있는 숫자 값으로 A · B = B · A 공식이 성립됩니다.
만약에 크기가 1인 벡터가 나오면 단위 벡터로 정의할 수 있습니다.
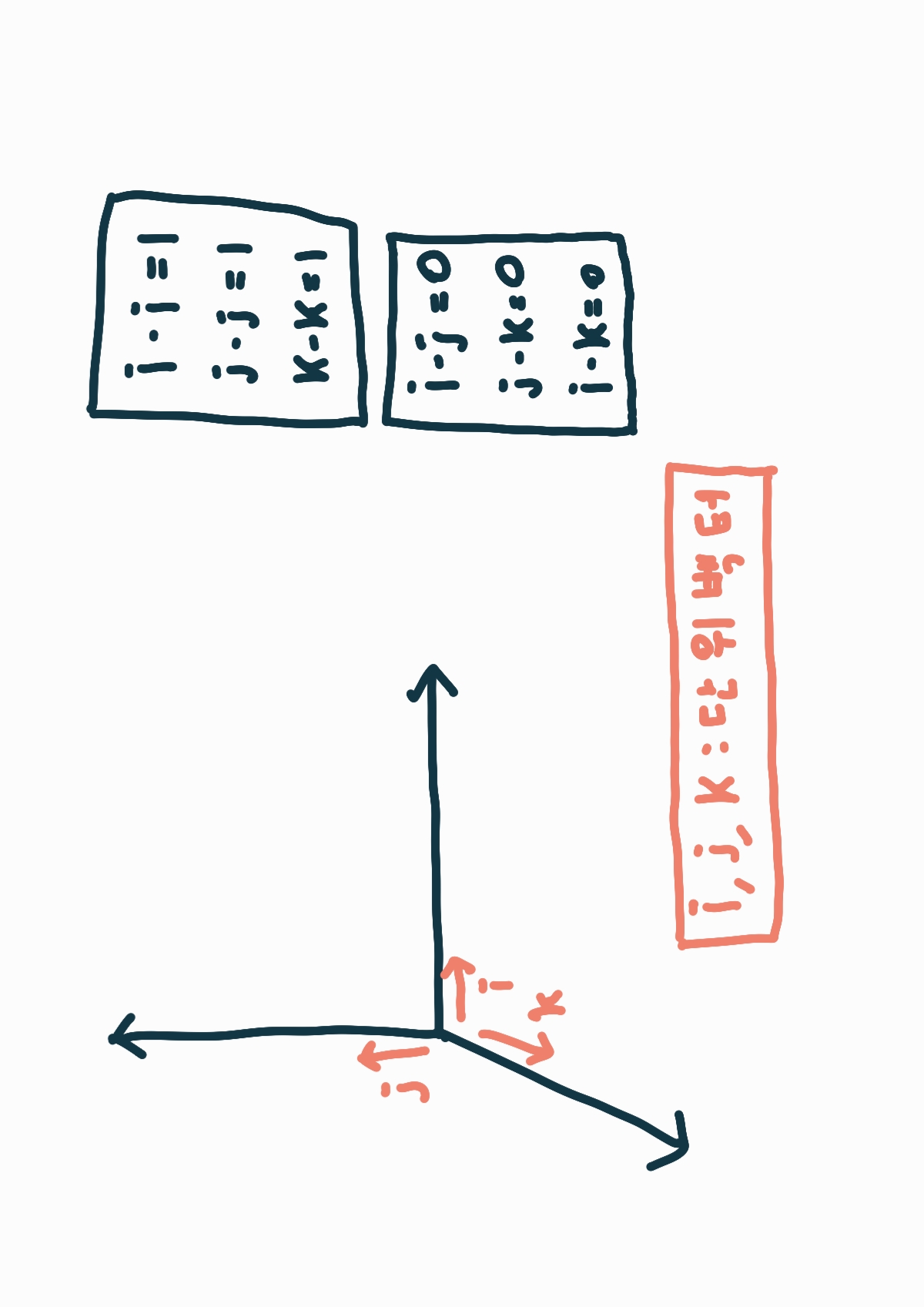
여기서 i, j, k는 3차원 공간에서 사용되는 기본적인 단위 벡터입니다.
벡터의 방향이 비슷하면 내적은 양수가 되고 방향이 반대라면 내적은 음수가 됩니다.
글자 양쪽에 절대값은 해당 요소에 길이와 크기를 나타냅니다.
또 다른 케이스의 단위 벡터 내적을 알아보겠습니다.
[A · B = |A| x |B| x cos θ]
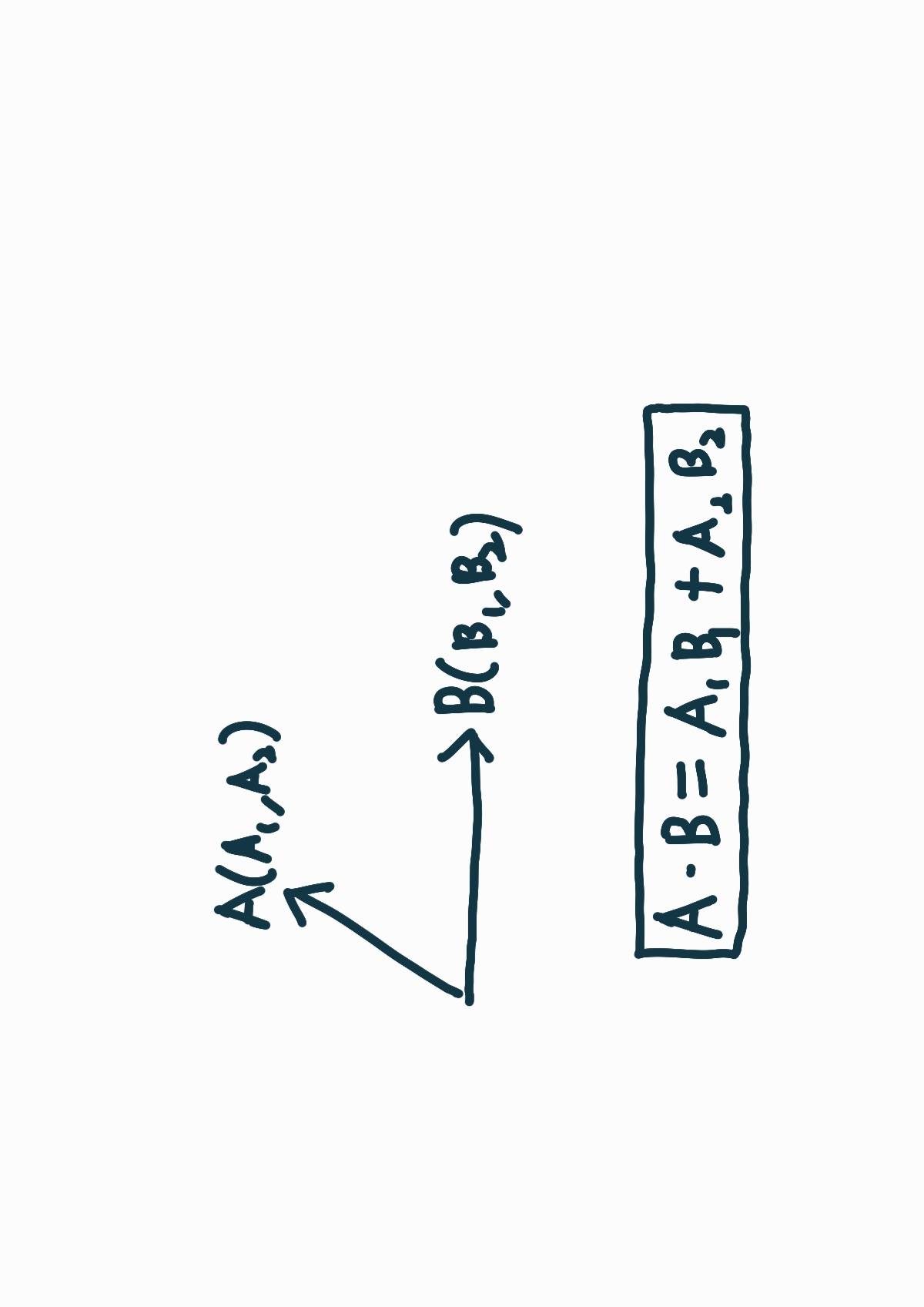
여기서 A1 , B1 , A2 , B2는 각각 벡터 A와 B의 구성요소입니다.
만약 A · B = (4i+3j)(2i-j)라면 값은 8-3으로 5가 됩니다.
벡터 a와 b가 수직으로 교차할 때 (cos 90º = 0) 내적은 0이 됩니다.
[A · B = A1B1 + A2B2]
벡터의 외적은 두 벡터의 크기와 방향을 이용하여 새로운 벡터를 생성하는 연산입니다.
계산 방식은 두 벡터 간의 행렬곱셈을 통해 이루어지고 3차원 좌표공간에서 정의합니다.
오른속 법칙을 이용해보면 A x B = - B x A로 교환법칙이 성립되지 않습니다.
그러나 결합법칙과 분배법칙은 가능합니다.
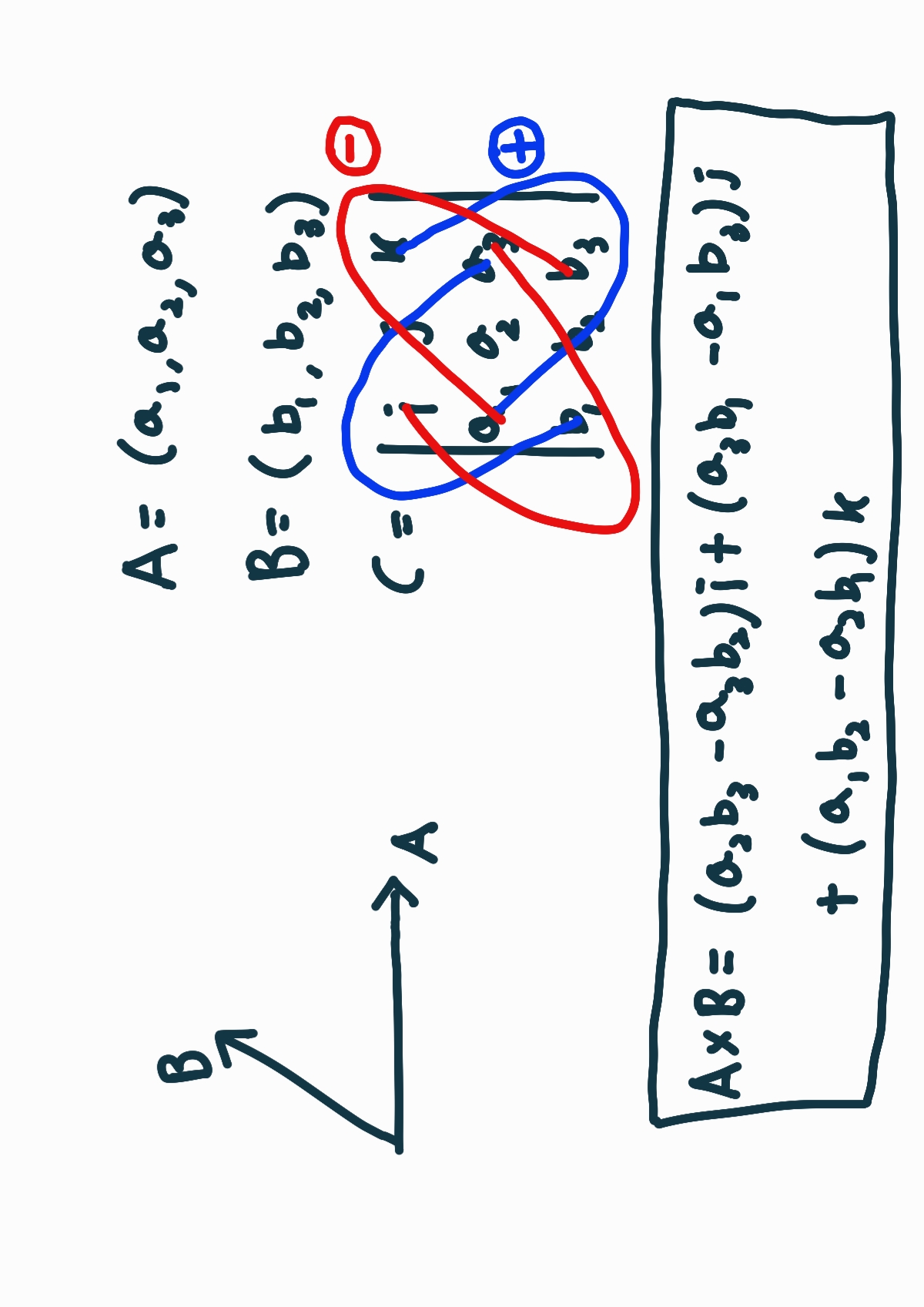
두 벡터 A, B의 외적을 행렬식으로 구했습니다.
[A x B = (a2b3-a3b2)i + (a3b1-a1b3)j + (a1b2-a2b1)k]
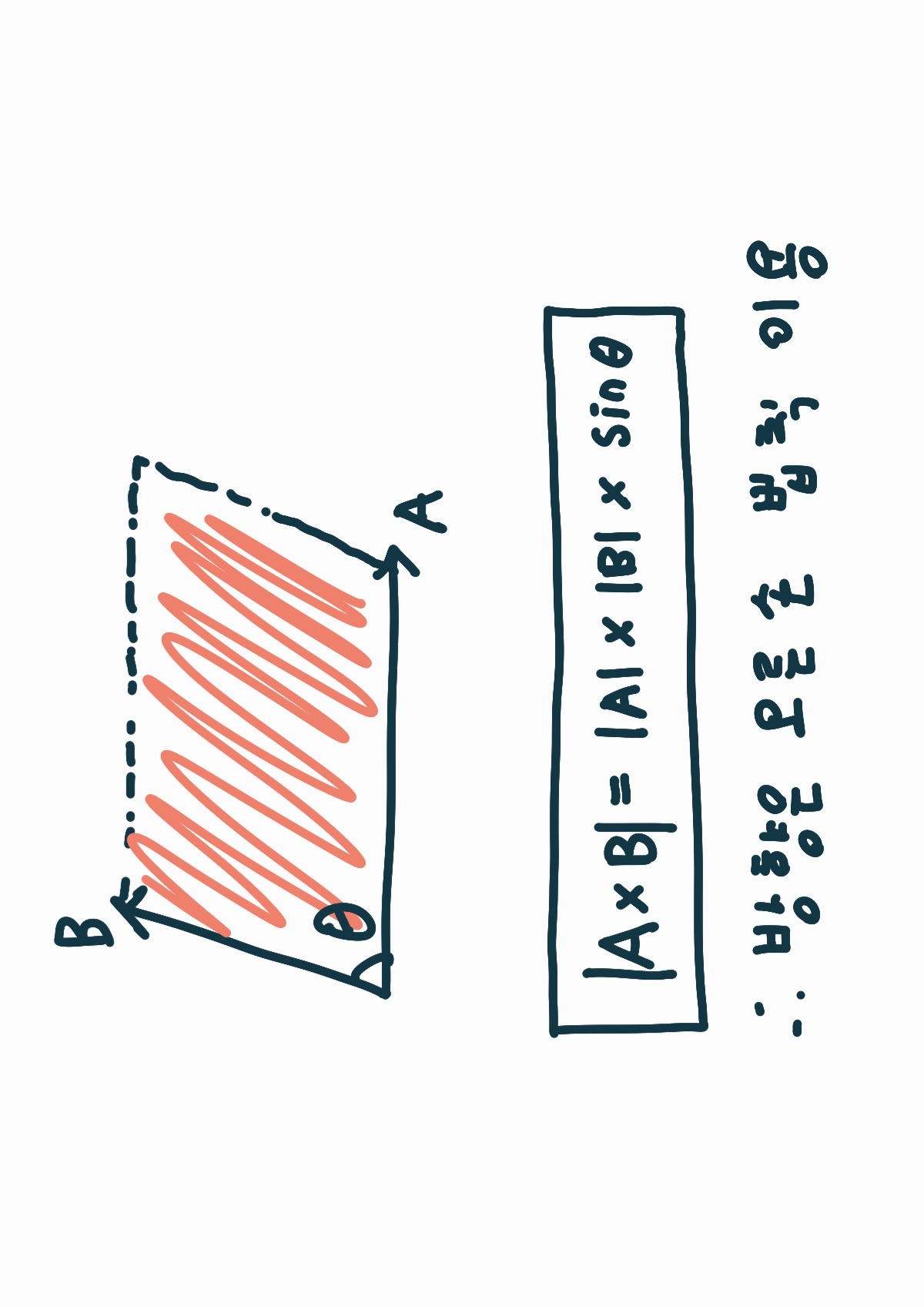
외적의 크기는 위의 식으로 계산이 가능하며 방향은 오른손 법칙으로 정리할 수 있습니다.
참고로 외적의 방향은 벡터 A, B와 수직이 되어야 합니다.
댓글 (0)
간편 댓글 작성





