
Physics 포스팅
Doyeon0430 | 2023년 09월 28일
이번시간에는 통계학에서 다양한 자료의 종류를 알아보겠습니다.
평균, 중앙값, 최빈값, 편차, 평균편차, 분산, 표준편차, 간편식, 사분위범위, 백분위수, Z점수에 대한 개념을 소개하겠습니다.
그럼 지금부터 포스팅을 시작합니다.
중심위치의 측도는 데이터 집합의 대표값 또는 중심 경향성을 나타내는 측도입니다.
.jpg)
수집된 자료의 중심적 위치를 대변합니다.
양적자료에서만 사용되며 관측한 자료의 값들을 x1부터 xn까지 있을 때
위의 수식처럼 정의할 수 있습니다.
모집단일 때 평균은 μ으로 표시하고 표본일 때 평균은 χ로 표시합니다.
대부분의 경우 자료는 표본입니다.

크기 순서에 따라 배열된 숫자들 중에서 중앙에 위치한 값을 나타냅니다.
이것 또한 양적 자료에서만 사용되면 홀수와 짝수에 따라 구하는 공식이 다릅니다.
.jpg)
자료 중에서 가장 자주 나오는 값을 나타내며 질적 자료나 양적 자료 모두 사용됩니다.
자료를 몇 개의 계급으로 나누어 가장 도수가 높은 계급(최빈 계급)의 중앙값을 최빈값이라고 합니다.
위 표에서 최빈 계급은 50~70이고 최빈값은 중간값인 60입니다.
산포의 측도는 데이터의 분산 또는 퍼짐 정도를 측정하는 데 사용되는 측도입니다.
산포는 작을수록 정밀한 데이터입니다.
아래 표를 통해 정확성과 정밀성에 차이점을 알 수 있습니다.
.jpg)
정확성은 데이터의 중심일치 여부를 정밀성은 데이터의 집중 여부를 나타냅니다.
.jpg)
편차는 모든 특성치로부터 평균값을 뺀 값이며 평균편차는 편차들의 절대값의 평균입니다.
여기서 편차들을 모두 합하면 항상 0이 되기 때문에 평균편차로 절대값의 평균을 구합니다.
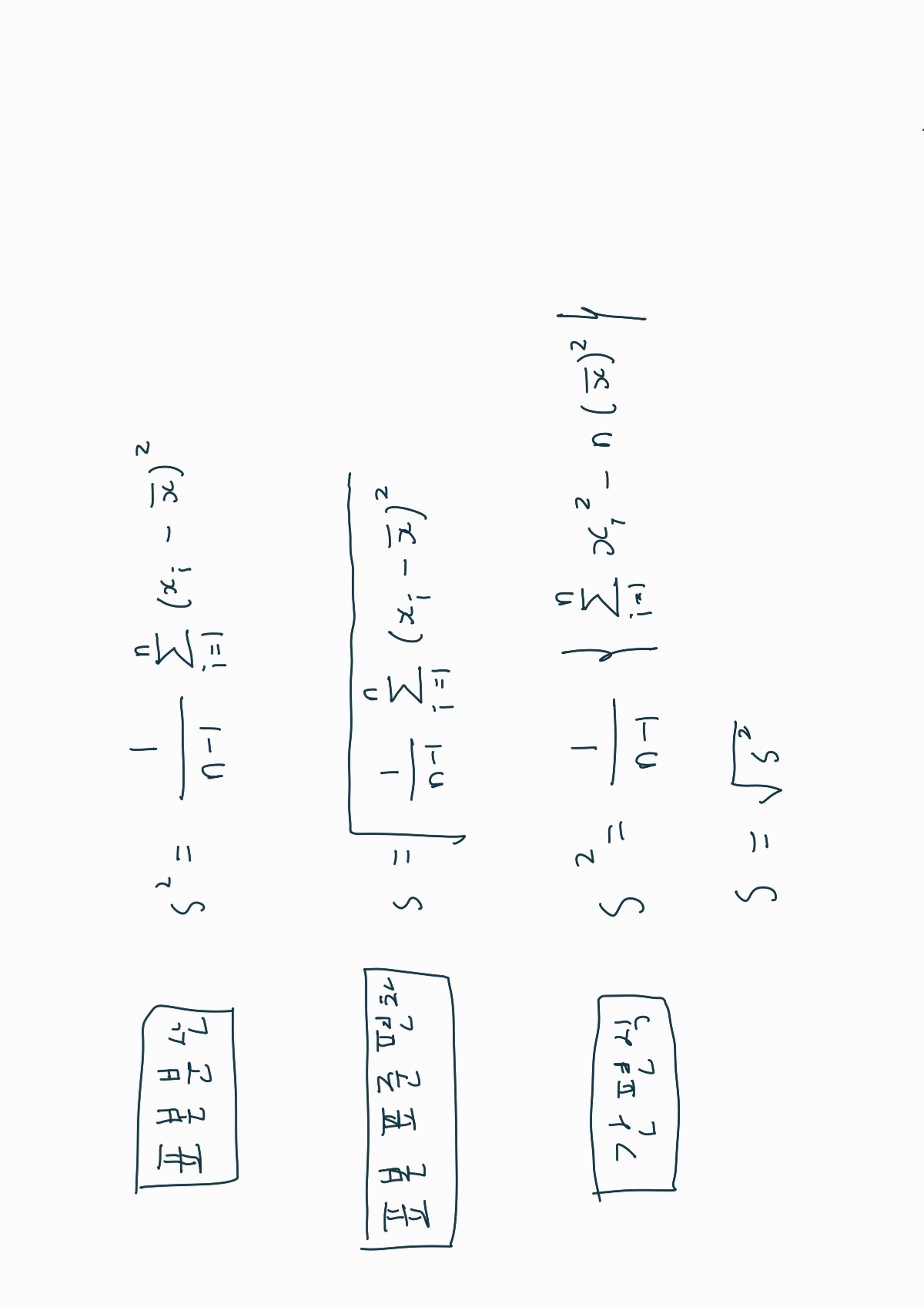
편차의 합 대신 편차의 제곱의 합을 사용합니다.
편차의 제곱의 합을 자료수로 나누어 사용하는게 분산입니다.
여기서 표본분산을 계산할 때 n 대신에 n-1로 자유도를 사용합니다.
분산에 표기는 모분산에서 σ2이며 표본분산에서 s2입니다.
표준편차에 표기는 모표준편차에서 σ이며 표본표준편차에서 s입니다.
.jpg)
.jpg)
표본분산과 간편식에 풀이 차이점입니다.
간펵식을 사용하면 보다 수월하게 값을 구할 수 있습니다.
.jpg)
사분위범위는 크기 순서에 따라 늘어 놓은 자료를 4등분하는 수입니다.
주로 자료가 두 극단적인 값의 차이를 나타낼 때 사용할 수 있습니다.
사분위범위 = 제3사분위수 - 제1사분위수위 공식을 통해 사분위범위를 나타냅니다.
자료에 이상점이 존재할 때 분산이나 표준편차보다는 그 이상점의 영향을 덜 받습니다.
그러나 모집단에서 사용하기 힘들어서 널리 사용하지 않습니다.
상대적 위치의 측도는 어떤 특정한 자료값이 주어진 자료의 어떤 위치에 있는지를 알 수 있게 해줍니다.
대표적으로 백분위수와 Z점수 등이 있습니다.
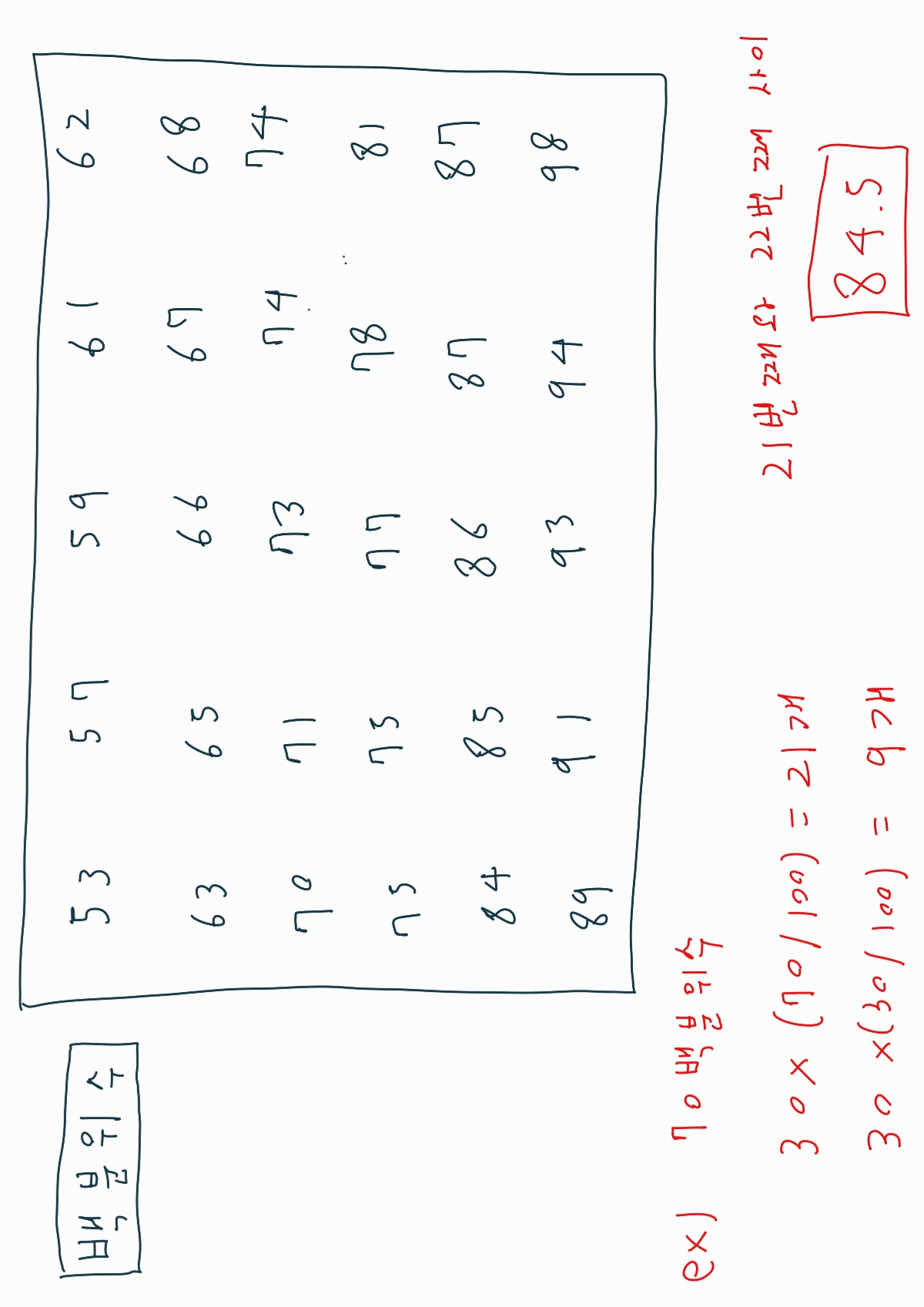
백분위수는 크기 순서에 따라 나열한 값들을 100 등분하는 수의 값입니다.
주로 자료의 크기가 30보다 큰 경우 사용해야 합니다.
제P백분위수는 자료값 중 P%가 그 값보다 작거나 같고 (100-P)%가 그 값보다 크거나 같게 하는 값위 예시에서 70백분위수보다 작은 자료값은 21개이고 큰 자료값은 9개입니다.
그렇기에 21번째와 22번째 중간값이 나옵니다.
.jpg)
측정한 자료값이 평균으로부터 표준편차의 몇 배만큼 떨어졌는지 측정합니다.
자료의 형태가 개개의 자료값이 아닌 집단회된 상태일 때 사용합니다.
.jpg)
전체 자료의 수가 29이며 중앙값은 크기 순서대로 나열하면 15번째가 나옵니다.
여기서 누적도수를 통해 15번째가 17.5~22.5 사이의 계급구간에 존재하는 것을 알 수 있습니다.
누적도수 15번째는 계급구간(17.5~22.5) 도수 중 6번째에 위치해 있습니다.
그렇게 중앙값을 구할 수 있습니다.
L은 그 계급의 시작점입니다. ex) 17.5
h는 그 계급의 간격입니다. ex) 22.5-17.5
i는 누적도수입니다. ex) 15
f는 i는 자료값이 속하는 계급의 도수입니다. ex) 8
a는 앞 계급구간까지 누적도수입니다. ex) 9
댓글 (0)
간편 댓글 작성





